赛尔号赛尔号计算解析系列文章(第二期):单双属性克制系数计算方法与n属性计算公式猜想,由橙汁带来的浓浓学术氛围的解析攻略来啦!想要自己尝试计算属性克制关系的小赛尔们可以来看看哦~
【文章大体介绍】
本文主要是介绍单属性与双属性的克制系数计算方法,解析常见的错误的计算方法加以改正,并根据单双属性推测推广n属性的算法。
在开始正文之前,我先来回答一些大家可能会问到的一些问题,这些问题的回答或许对您阅读文章有一定帮助。
Q:这种文章岂不是把简单的问题复杂化?
A:从实践中总结经验,由特殊推广到一般,将实践经验上升为理论成果,最终还要用理论指导实践活动,并在实践中检验与发展真理。这大概就是我们所说的“辩证唯物主义认识论”吧。数学模型的提出不是将简单的问题复杂化,而是将具体的事物抽象出其本质,在更深的层面认识世界,并用以更好地改变世界。
Q:只是玩一个游戏至于这样吗?
A:对于一个游戏,是否值得花费精力对其进行更加彻底地剖析呢?或许每个人的想法不同,对于游戏,怎样去玩每个人有不同的见解。对游戏的运行机制进行分析何尝不是一种游玩游戏的方式呢?
Q:我一点儿都看不懂怎么办?我该如何阅读这篇文章?
A:由于使用了数学函数工具,所以或许对于一部分玩家阅读起来比较难以理解,不过我相信看这篇文章的小伙伴都是学霸,仔细阅读一定可以看懂的。一般玩家阅读完文章可以掌握单属性与双属性的克制系数计算方法,为了帮助大家理解,文章中除了数学表达式,也有很多文字描述,并且还有实战举例。对于数学感兴趣的小伙伴可以阅读一下n属性克制系数计算公式,这一部分比较难理解。对于编程感兴趣的小伙伴可以看一下最后的C++代码。如果你实在看不懂数学猜想和代码那些部分,你可以了解一下单双属性的计算方法。
Q:写这篇文章的目的是什么?
A:主要是为了帮助大家搞清楚单属性与双属性的克制系数的计算方法,并纠正大家常犯的错误的计算方法,帮助大家了解一些游戏运行的机制,并讲述一下关于n属性系数计算公式的猜想。
【单双属性克制系数计算方法】
接下来开始正文。首先,我们来了解一下游戏中实战的单属性与双属性克制系数计算方法。
1、单属性攻击单属性的克制系数:
查表获得,系数只能为0(无效)、0.5(微弱)、1(普通)、2(克制)这四个数。
假设攻击方单属性为A,防守方单属性为B,A攻击B的克制系数为x1 ,则对于A打B的克制系数f(1,x1),有f(1,x1)= x1 。
2、双属性攻击单属性的克制系数:
如果攻击方的两个属性打防守方单属性的两个系数都是2,那么该双属性打单属性的系数为2+2=4;
如果攻击方的两个属性打防守方单属性的两个系数中至少有一个是0,那么双属性打单属性的系数为两个系数之和÷4;
如果不是以上两种情况,即其他的情况,那么双属性打单属性的系数为两个系数之和÷2。
假设攻击方双属性为A·B,防守方单属性为C,A攻击C的克制系数为x1,B攻击C的克制系数为x2 ,则对于A·B打C的克制系数f(2,x1,x2)。
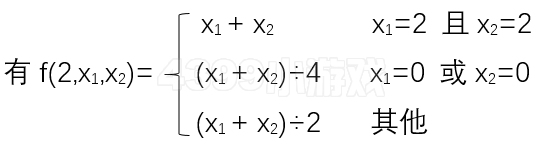
3、单属性攻击双属性的克制系数:
如果攻击方单属性属性打防守方的两个属性的两个系数都是2,那么该单属性打双属性的系数为2+2=4;
如果攻击方单属性打防守方的两个属性的两个系数中至少有一个是0,那么单属性打双属性的系数为两个系数之和÷4;
如果不是以上两种情况,即其他的情况,那么单属性打双属性的系数为两个系数之和÷2。
假设攻击方单属性为A,防守方双属性为B·C,A攻击B的克制系数为x1,A攻击C的克制系数为x2 ,则对于A打B·C的克制系数f(2,x1,x2)。
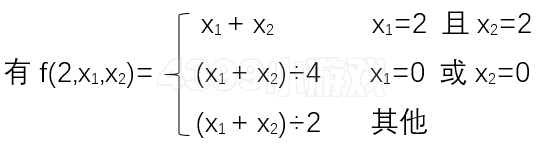
4、双属性攻击双属性的克制系数:
用攻击方的双属性打防守方的两个属性的系数加和,再÷2。
注意,不要弄反,一定要用攻击方双属性打防守方2个组成的单属性的系数之和进行计算,也就是说拆分的是防守方的两个属性。
假设攻击方单属性为A·B,防守方双属性为C·D,A·B攻击C的克制系数为f1(2,x11,x12),A·B攻击D的克制系数为f2(2,x21,x22) ,则对于A·B打C·D的克制系数g[2, f1(2,x11,x12), f2(2,x21,x22)],有g[2, f1(2,x11,x12), f2(2,x21,x22)]= [f1(2,x11,x12) + f2(2,x21,x22)] ÷ 2。
【举例说明与验证】
可能看理论公式比较抽象,不好理解,下面我们讲几个例子说明一下。
例1】计算圣灵·地面系打电·火系的克制系数。
解:经查表可知,圣灵系打电系的系数x11为2,地面系打电系的系数x12为2,圣灵系打火系的系数x21为2,地面系打火系的系数x22为2,
则圣灵·地面系打电系的系数f1(2,x11,x12)= x11 + x12 = 2+2 = 4 , 圣灵·地面系打火系的系数f2(2,x21,x22)= x21 + x22 = 2+2 = 4 ,
进而圣灵·地面系打电·火系的系数g[2, f1(2,x11,x12), f2(2,x21,x22)]= [f1(2,x11,x12) + f2(2,x21,x22)] ÷ 2 =( 4+4 ) ÷ 2 = 4。
易错点:将单属性与双属性的算法强加给双属性与双属性的算法上,错认为两个4倍会变成8倍。
例2】计算圣灵·超能系打电·火系的克制系数。
解:经查表可知,圣灵系打电系的系数x11为2,超能系打电系的系数x12为1,圣灵系打火系的系数x21为2,超能系打火系的系数x22为1,
则圣灵·超能系打电系的系数f1(2,x11,x12)= x11 + x12 = ( 2+1 )÷2 = 1.5 , 圣灵·超能系打火系的系数f2(2,x21,x22)= x21 + x22 = ( 2+1 ) ÷ 2 = 1.5,
进而圣灵·超能系打电·火系的系数g[2, f1(2,x11,x12), f2(2,x21,x22)]= [f1(2,x11,x12) + f2(2,x21,x22)] ÷ 2 =( 1.5+1.5 ) ÷ 2 = 1.5。
易错点:错将攻击方的两个属性拆分,然后用两个攻击方的单属性打防守方双属性的系数进行计算,会错误地得到结果(4+1)÷2=2.5。
下面,为了验证例2计算结果的正确性,我们进行实战测试。(感谢阿狸与逆天帮助数据测试)
测试采用的防守方的火电王和圣缪的特防都是一样的,而且攻击方的缪斯都是首回合出招打伤害,打完就刷新重测,可以保证严格控制变量,即唯一变量为属性克制系数。由于圣缪第五技能效果“攻击时造成的伤害不会出现微弱(克制关系为微弱时都变成普通)”,因此在实战中,圣缪第五技能打对方圣缪的克制系数为1,理论上打火电王的克制系数为1.5。
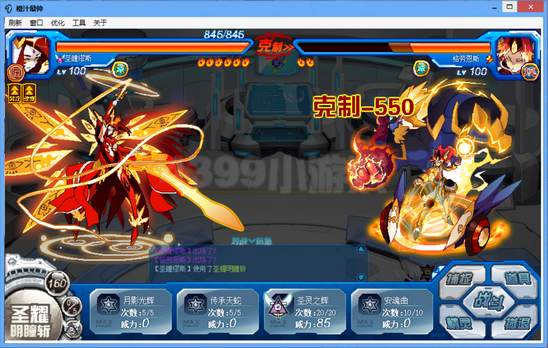
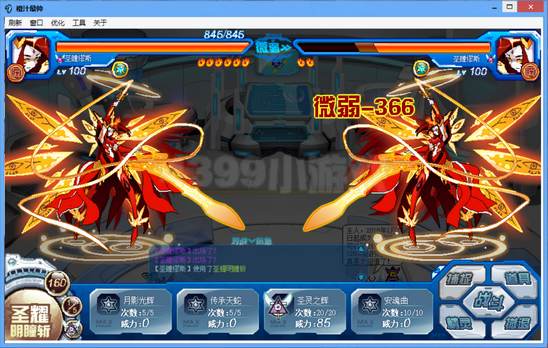
由于时间匆忙,于是只打了6次(12场)进行测试,当然打的越多,算平均值就越准确。以下是这12场的伤害测试结果,表格中平均值为6次平均伤害取值,理论值为由伤害计算公式计算(我是用自制的伤害计算器算的)而来的理论平均伤害值。
| 伤害测试 | 格劳恩斯 | 圣瞳缪斯 | 伤害倍数 |
| 第一次 | 611 | 395 | 1.54683544 |
| 第二次 | 585 | 428 | 1.36682243 |
| 第三次 | 547 | 379 | 1.44327177 |
| 第四次 | 550 | 366 | 1.50273224 |
| 第五次 | 598 | 374 | 1.59893048 |
| 第六次 | 628 | 422 | 1.48815166 |
| 平均值 | 586.5 | 394 | 1.48857868 |
| 理论值 | 595 | 397 | 1.50000000 |
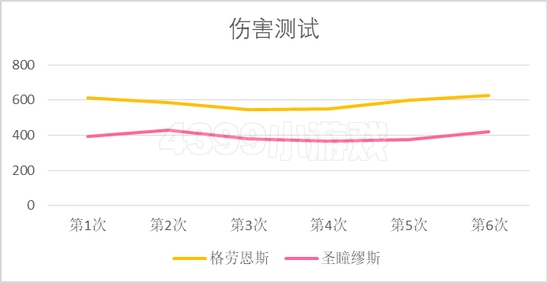
做好表格,我们将数据的折线图画出来,可以看到,打火电王(1.5倍)的伤害在600左右,打圣缪(1倍)的伤害在400左右,相除得到的结果正好是1.5倍理论值。






 考沃莱恩
考沃莱恩 糖果皮皮
糖果皮皮 水晶皮皮
水晶皮皮 机魂核心·卡尔玛
机魂核心·卡尔玛 不熟不要钱
不熟不要钱 理发
理发 混沌沧岚
混沌沧岚 噩梦之源-魂歌入梦
噩梦之源-魂歌入梦 迷你世界
迷你世界 创造与魔法
创造与魔法 逃跑吧少年
逃跑吧少年 洛克王国
洛克王国 生死狙击
生死狙击 奥奇传说
奥奇传说 4399火线精英
4399火线精英 造梦无双
造梦无双 我的世界
我的世界 王者荣耀
王者荣耀 和平精英
和平精英 自走棋
自走棋 天涯明月刀手游
天涯明月刀手游 使命召唤手游
使命召唤手游 英雄联盟
英雄联盟 原神
原神 方舟生存进化
方舟生存进化 明日之后
明日之后